[15 April 2008]
For reasons too complicated to go into just now (I tried, and it takes paragraphs and paragraphs), I have found myself thinking lately about a grammar manipulation process well known to be possible and wondering how to do it in fact.
Background
Sometimes what you have is a context-free language L, but what you need is a related regular language. Or, more precisely, what you have is a context-free grammar for L, and what you need is a regular grammar or an FSA or a regular expression that recognizes either the largest practicable regular sub-language of L or the smallest regular super-language of L. You might need this because the context-free grammar, in all its hairy glory, is too difficult to handle with the limited resources at your disposal. (The tractable-sublanguage approach was pioneered by students of natural languages, back when they were trying to make the equivalent of an 80386 parse English.) Or you might need it because you want to define an element or attribute for expressions of some kind defined by a context-free grammar, and you want to define a simple type for them, for use with XSD, or you want to use Simon St. Laurent’s regular fragmentation or similar tools to describe them, but the tools (like the XSD pattern facet) only deal with regular expressions, not context-free grammars.
Since regular grammars are weaker (or dumber) than context-free grammars, the question turns into: how can we most usefully go about dumbing down a context-free grammar to make it into a regular grammar?
The largest practicable regular sub-language
Now, it’s reasonably well known that for any context-free language which allows arbitrarily deep nesting of structures (that is, for any context-free language at all — if it doesn’t allow arbitrarily deep nesting, the language isn’t context-free), it’s possible to describe a related regular language which allows some bounded amount of nesting.
For example: the language of arithmetic expressions defined by this grammar is context-free:
expression = term (add-op term)*
term = factor (mul-op factor)*
factor = NUMBER | VAR-REF | '(' expression ')'
add-op = '+' | '-'
mul-op = '*' | '/'
A similar language that allows nesting of parenthesized expressions only up to some fixed depth is regular, not context-free, and can be recognized with a finite-state automaton or described with a regular expression. And every sentence in the regular language is a sentence in the original context-free language.
This fact has been exploited before now to make certain parsing and grammar-management tasks more tractable. I read about it first (if memory serves) in Grune and Jacobs, Parsing techniques: A practical guide, who cite a number of papers, most of which I have not read. But while they provide a clear high-level description of how the necessary grammar transformation works, they don’t go into any detail about how to perform the transformation in practice for arbitrary grammars. So it’s been in the back of my mind for some time to think it through and see if I could reduce it to code.
The smallest regular super-language
Sometimes, the regular language you want is not a sub-language, but a super-language. Suppose we wanted to write a regular expression that would accept all legal arithmetic expressions and as few other strings as possible. (If you’re defining a simple type for arithmetic expressions, you don’t want it rejecting things just because the parentheses are nested too deep. So you need a superlanguage, not a sub-language.) The nature of the context-free / regular distinction is that such a super-language would not require parentheses to match up correctly. But it should be possible to enforce some of the other rules relating to parentheses: we want strings like “(3 +)” or “4 (* x)” to be rejected, because in the original grammar operators are not allowed to be adjacent to parentheses in this way, and you don’t need a context-free grammar to enforce those rules.
As it happens, the regular expression (*d+()|[+-*/]d+)* comes pretty close to capturing the rules. (For simplicity, I have just written “d+” for the places where the original grammar has NUM or VAR-REF.) That is, unless I have botched something somewhere, any string legal against the original grammar will be legal against this regular expression, and nothing else will except strings that would be correct except that their parentheses are messed up.
Towards a method
Given a particular context-free grammar, it’s generally possible to sit down with it and cipher out how to dumb it down into a regular grammar for fixed depth, or a regular grammar for arbitrary depth but no checks on parenthesis nesting. But how do you do it for arbitrary grammars, methodically and mechanically? How do you reduce it to code?
I daresay it’s in the literature, but I haven’t read much of the relevant literature; I expect to, when I can, but it was more fun to try to solve the problem from scratch, armed only with Grune and Jacobs’ concise description
Even (finite) context-dependency can be incorporated: for languages that require the verb to agree in number with the subject, we duplicate the first rule:
MainClause -->
SubjectSingular VerbSingular Object
| SubjectPlural VerbPlural Object
and duplicate the rest of the grammar accordingly. The result is still regular…. We replicate the grammar the desired number of times and remove the possibility of further levels from the deepest level. Then the deepest level is regular, which makes the other levels regular in turn. the resulting grammar will be huge but regular and will be able to profit fom all simple and efficient techniques known for regular grammars. The required duplications and modifications are mechanical and can be one by a program.
I don’t have code yet. But I do have a sketch of a methodical approach. Some of these steps probably need further explanation, which I do not have time to provide today.
- Find the set of non-terminals in the grammar that are reachable from themselves (call these cyclic non-terminals).
- To each production for a relevant non-terminal (details below), add a synthesized attribute to the grammar, to show the nesting level for that non-terminal. Non-terminals are relevant if one of the cyclic non-terminals is reachable from them.
- Draw the CFG as an augmented transition network (this amounts to drawing each rule as an FSA, with terminals or non-terminals labeling the arcs).
- Using (an adaptation of) the Thompson algorithm, combine the FSAs from the transition network into a single FSA with epsilon transitions as necessary, and only terminals labeling the arcs. Keep track of the attributes using whatever additions to the usual tools your wit can provide. Me, I use counting FSAs as I described them in 2004; I still can’t believe that work is new, but I still haven’t found anything else in that vein.
- Eliminate epsilon transitions in the usual way, to clean things up. If your heart is strong, you may also be able to merge states that clearly can be merged safely, but I don’t know how to define that test formally just yet.
- You now have a fairly standard counting FSA; it can readily be re-transcribed into a counting regular attribute grammar (CRAG).
- To generate a regular sub-language, assign a maximum value to each counter; you now have an attribute grammar over a finite lattice and can generate a normal (non-attributed) grammar in the obvious way.
- To generate a regular super-language, just ignore (or: delete) the guards and counters.
Strictly speaking, you can generate both the sub- and the super-language as soon as you have the attribute grammar of step
Let me illustrate using the arithmetic expression grammar above.
First, note that expression, term, and factor are all cyclic, and nothing else is. In this particular case, we actually only need one counter, but it does no harm to add all three. For brevity, I’ll abbreviate the non-terminals to single letters.
e(i,j,k) = t(i+1,j,k) (a t(i+1,j,k))*
t(i,j,k) = f(i,j+1,k) (m f(i,j+1,k))*
f(i,j,k) = NUMBER | VAR-REF | '(' e(i,j,k+1) ')'
a = '+' | '-'
m = '*' | '/'
The result of drawing a transition network (not shown) and then mushing it all together, after minimization, with guards and counter operations, is something like this: 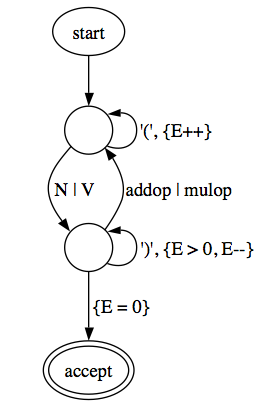
A counting regular attribute grammar for this, with e(0) the start symbol, is:
e(n) = '(' e(n+1)
e(n) = NUM q(n)
e(n) = VAR-REF q(n)
q(n) = [+-*/] e(n)
q(n) = {n > 0} ')' q(n-1)
q(n) = {n = 0} ''
(The last line could of course be written “q(0) = ''”, but for reasons I haven’t figured out the form with the explicit and verbose guard seems better, perhaps clearer. Maybe it is.)
This can be multiplied out in the obvious way to produce an unattributed grammar which accepts two levels of parenthesized expressions:
e = '(' e1
e = NUM q
e = VAR-REF q
q = [+-*/] e
q = ''
e1 = '(' e2
e1 = NUM q1
e1 = VAR-REF q1
q1 = [+-*/] e1
q1 = ')' q
e2 = NUM q2
e2 = VAR-REF q2
q2 = [+-*/] e2
q2 = ')' q1
And the smallest regular superlanguage appears to be
e = '(' e
e = NUM q
e = VAR-REF q
q = [+-*/] e
q = ')' q
q = ''
Some open questions and follow-on topics:
- Can a formally satisfactory definition be given which explicates the intuitive notion of the ‘smallest regular super-language’?
- If so, can it be proven that the construction above produces a grammar (an FSA, a regular expression) which in fact accepts the smallest regular superlanguage?
- To check this, I really ought to turn this into code; if any readers of this have a use for such code in Prolog or XSLT, let me know.
- It would be interesting to use this technique to write simple types for approximations of arithmetic expressions, and XPath expressions, and various other specialized types that in principle require context-free grammars. I foresee a union type with first a large regular subset, then the smallest regular superset, then arbitrary strings.
- This whole thing came up because I was worrying about issues relating to test cases for grammars; it would be nice to try to apply this work there.

